A new company sells customizable cases for tablets and smartphones. Each case comes in a variety of colors and can be personalized for an additional fee with images or a monogram. A customer can choose not to personalize or could choose to have one, two, or three images or a monogram. The customer can choose the order of the images and the letters in the monogram. The company is working with an agency to develop a marketing campaign with a focus on the huge number of options they offer. Counting the possibilities is challenging!
We encounter a wide variety of counting problems every day. There is a branch of mathematics devoted to the study of counting problems such as this one. Other applications of counting include secure passwords, horse racing outcomes, and college scheduling choices. We will examine this type of mathematics in this section.
The company that sells customizable cases offers cases for tablets and smartphones. There are \(3\) supported tablet models and \(5\) supported smartphone models. The Addition Principle tells us that we can add the number of tablet options to the number of smartphone options to find the total number of options. By the Addition Principle, there are \(8\) total options, as we can see in Figure \(\PageIndex\).
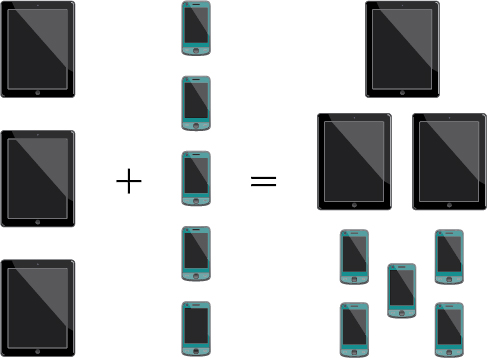
Figure \(\PageIndex\)
According to the Addition Principle, if one event can occur in \(m\) ways and a second event with no common outcomes can occur in \(n\) ways, then the first or second event can occur in \(m+n\) ways.
There are \(2\) vegetarian entrée options and \(5\) meat entrée options on a dinner menu. What is the total number of entrée options?
Solution
We can add the number of vegetarian options to the number of meat options to find the total number of entrée options.
There are \(7\) total options.
A student is shopping for a new computer. He is deciding among \(3\) desktop computers and \(4\) laptop computers. What is the total number of computer options?
The Multiplication Principle applies when we are making more than one selection. Suppose we are choosing an appetizer, an entrée, and a dessert. If there are \(2\) appetizer options, \(3\) entrée options, and \(2\) dessert options on a fixed-price dinner menu, there are a total of \(12\) possible choices of one each as shown in the tree diagram in Figure \(\PageIndex\).
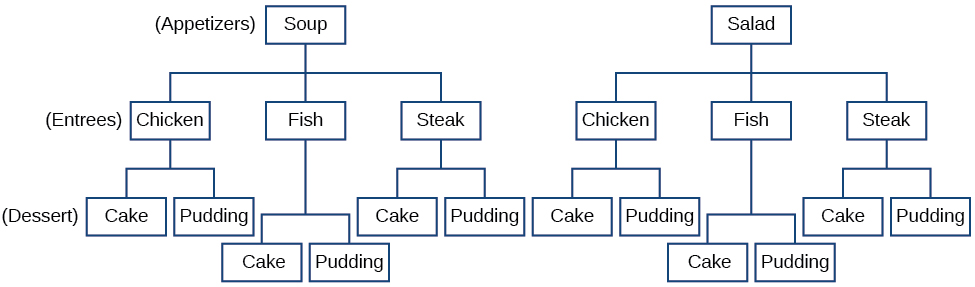
Figure \(\PageIndex\)
The possible choices are:
We could also conclude that there are \(12\) possible dinner choices simply by applying the Multiplication Principle.
According to the Multiplication Principle, if one event can occur in \(m\) ways and a second event can occur in \(n\) ways after the first event has occurred, then the two events can occur in \(m×n\) ways. This is also known as the Fundamental Counting Principle.
Diane packed \(2\) skirts, \(4\) blouses, and a sweater for her business trip. She will need to choose a skirt and a blouse for each outfit and decide whether to wear the sweater. Use the Multiplication Principle to find the total number of possible outfits.
Solution
To find the total number of outfits, find the product of the number of skirt options, the number of blouse options, and the number of sweater options.
There are \(16\) possible outfits.
A restaurant offers a breakfast special that includes a breakfast sandwich, a side dish, and a beverage. There are \(3\) types of breakfast sandwiches, \(4\) side dish options, and \(5\) beverage choices. Find the total number of possible breakfast specials.
Answer
There are \(60\) possible breakfast specials.
The Multiplication Principle can be used to solve a variety of problem types. One type of problem involves placing objects in order. We arrange letters into words and digits into numbers, line up for photographs, decorate rooms, and more. An ordering of objects is called a permutation.
To solve permutation problems, it is often helpful to draw line segments for each option. That enables us to determine the number of each option so we can multiply. For instance, suppose we have four paintings, and we want to find the number of ways we can hang three of the paintings in order on the wall. We can draw three lines to represent the three places on the wall.
There are four options for the first place, so we write a \(4\) on the first line.
After the first place has been filled, there are three options for the second place so we write a \(3\) on the second line.
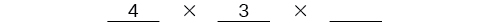
After the second place has been filled, there are two options for the third place so we write a \(2\) on the third line. Finally, we find the product.
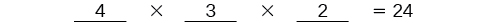
There are \(24\) possible permutations of the paintings.
At a swimming competition, nine swimmers compete in a race.
Solution
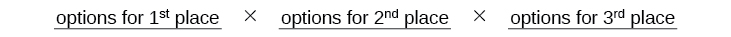There are \(9\) options for first place. Once someone has won first place, there are \(8\) remaining options for second place. Once first and second place have been won, there are \(7\) remaining options for third place. 
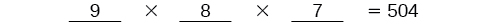Multiply to find that there are \(504\) ways for the swimmers to place.
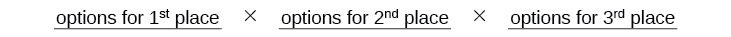We know Ariel must win first place, so there is only \(1\) option for first place. There are \(8\) remaining options for second place, and then \(7\) remaining options for third place. 
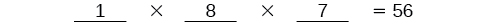Multiply to find that there are \(56\) ways for the swimmers to place if Ariel wins first.
There are \(9\) choices for the first spot, then \(8\) for the second, \(7\) for the third, \(6\) for the fourth, and so on until only \(1\) person remains for the last spot.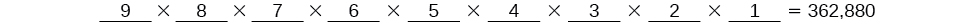 
There are \(362,880\) possible permutations for the swimmers to line up.Analysis
Note that in part c, we found there were \(9!\) ways for \(9\) people to line up. The number of permutations of \(n\) distinct objects can always be found by \(n!\).
A family of five is having portraits taken. Use the Multiplication Principle to find the following:
Answer b
Answer c
